前回は、リスクの意味についてお話ししました。
今回は、モンテカルロシミュレーションについてお話しします。
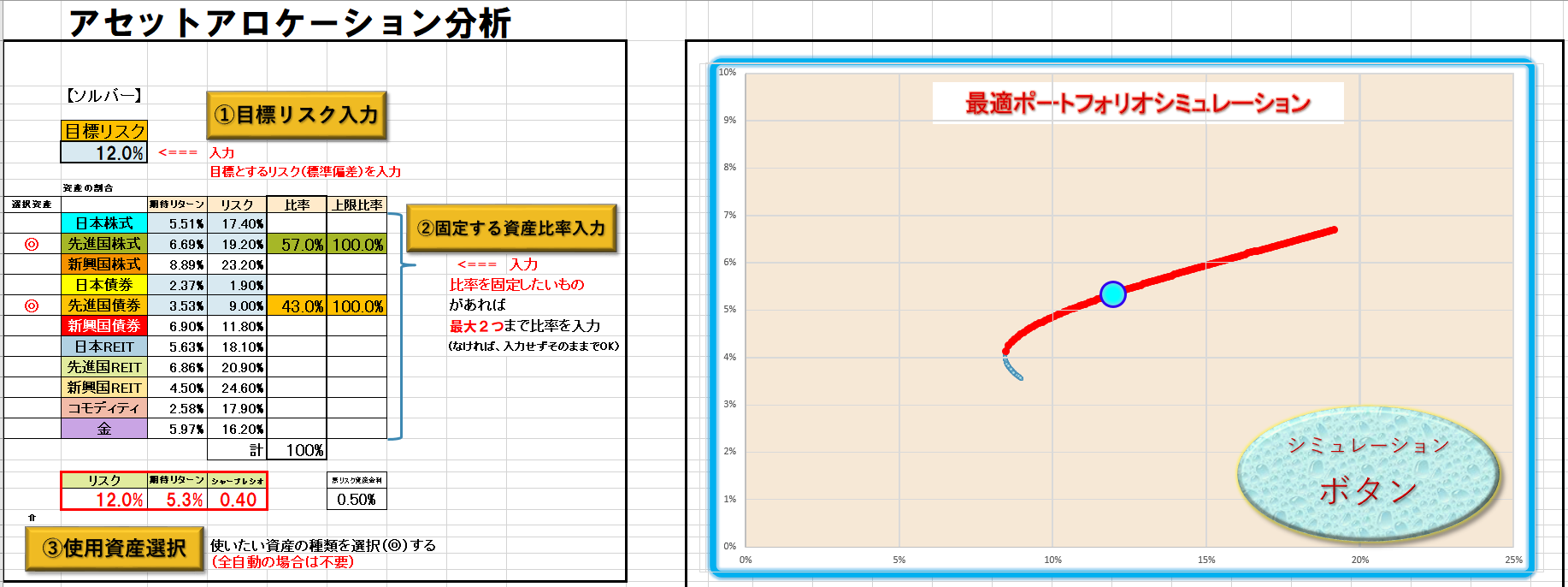
さて、以下のようなポートフォリオの将来の姿をシミュレーションしてみましょう。
シミュレーションにはモンテカルロシミュレーションという手法を使います。
モンテカルロという言葉は、フランスの地中海沿岸のニースの近くのモナコ公国の一地区名。国営カジノで有名な場所。
ランダムな条件を設定して、試行した結果を集計して統計的に分析する手法がモンテカルロシミュレーション。

100万円を先進国株式に連動する投資信託と先進国債券に連動する債券にそれぞれ70.0%、30.0%の割合で投資することによって将来資産価値はどれだけになっているかをモンテカルロシミュレーションでシミュレーションしてみます。
このポートフォリオの期待リターンは5.7%でリスクは14.0%です。
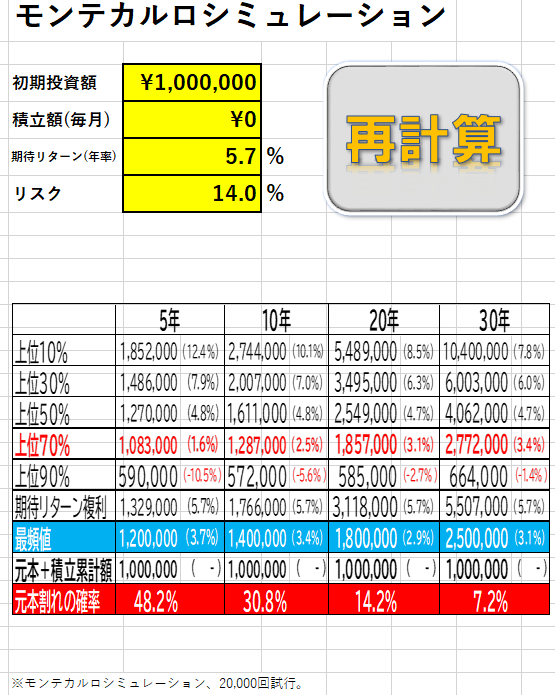
例えば、5年目の資産価格がいくらになっているかのシミュレーションをする場合はこうです。
最初に投資した金額100万円について、1年後いくらのリターンが生まれるかを計算します。
利回りは、5.7%±14.0%の範囲内の任意の数値を取ります。
どの数値を取るかは乱数を使ってランダムな数値を設定します。
乱数というのは、さいころを振るように規則性のないランダムな数値を取ることです。
この前提としては、株価はランダムウォークするという前提があります。
ランダムウォークというのは、酔っ払いが千鳥足で歩くように右へ行くのか左へ行くのかは全く予測できない動きをするという意味です。
乱数を使って価格のランダムウォークを再現します。
1年後の価格にリターンが上乗せされた金額を元本として、5.7%±14.0%の範囲内の任意の数値を乱数を使って取り、リターンを計算します。
これで2年後の元本にリターンを上乗せした金額が求められます。
そして、その金額を元本として、5.7%±14.0%の範囲内の任意の数値を乱数を使って取り、リターンを計算します。
これで3年後の元本にリターンを上乗せした金額が求められます。
そして、その金額を元本として、5.7%±14.0%の範囲内の任意の数値を乱数を使って取り、リターンを計算します。
これで4年後の元本にリターンを上乗せした金額が求められます。
そして、その金額を元本として、5.7%±14.0%の範囲内の任意の数値を乱数を使って取り、リターンを計算します。
これで5年後の元本にリターンを上乗せした金額が求められます。
このような計算を、1年目で2万個、2年目でも2万個、3年目でも2万個、4年目でも2万個、5年目でも2万個行います。
すると、5年目に取りうる資産価格が2万個シミュレーションできることになります。
その2万個の結果から金額の範囲別の確率や元本割れの確立などを計算しています。
実際は、30年分の計算をするので、2万個×30年分=60万個のセルに計算式を埋め込んであります。
コンピューターの性能にもよりますが、これを数秒から数十秒で行ってしまうことができます。
多分、10年ほど前だとこれほどたくさんの計算を一つのシートで行うのはかなり難しかったのではないかと思います。
また、パソコンの性能も今ほどではないのでもっと時間がかかったりしたでしょう。
しかし、現在はソフトウェア(エクセル)の性能もハードウェア(パソコン、CPU)の性能も上がったため簡単に計算することができるようになっています。
今回は、モンテカルロシミュレーションについてお話ししました。
次回は、分散の条件を変えた場合のシミュレーション結果を比較してみましょう。
では、お楽しみに。