こんにちは。FP相談ねっと認定FPの大地恒一郎です。
前回まで6回にわたって、投資信託の分野に絞ったFP3級過去問解説を行ってきました。
今回以降は、「金融資産運用」の過去問から何題かピックアップして解説していこうと思います。
ですが、その前にきんざいのFP3級テキストを眺めていましたら、「金融資産運用」ではなく「ライフプランニング」の分野で大切になってくる6つの係数が、突然目に入りました。
こういう係数の名前は普段目にしないものなので、勉強する上では少し混乱するのではないか、と思い、今回取り上げてみることにしました。
今までの過去問を調べてみると、ほぼ毎回のように1問出題されているようです。
2017年以降では、2019年5月試験で出題されなかったようですが、その他では、【第2問】の最初の問題(31)で出題されることが多いようです。
今度の9月試験で出題されるかどうかは分かりませんが、FPとしてライフプランニングには欠かせない係数ですので、押さえておきたいところです。
ということで、まず2017年5月に実施された試験問題から見ていきましょう。
2017年5月28日実施 第2問(31)
註:出題年が間違っていましたので、訂正しました。(平成28年✕⇒2017年(平成29年)〇)
一定の利率で複利運用しながら、毎年一定金額を積み立てた場合の一定期間経過後の元利合計額を試算する際、毎年の積立額に乗じる係数は、( )である。
(1) 減債基金係数
(2) 年金現価係数
(3) 年金終価係数
第2問(31)解説
この種の問題は、各係数の意味をきちんと覚えておかないと、なかなか答えづらいところではありますが、そうはいっても何かコツがあるのではないかと考えたくなります。
まずは正攻法で、一つ一つの意味を押えていきましょう。
(1)の減債基金係数は、「将来の目標金額から毎年の積立金額を算出する際に利用」する係数です。あまり普段使わない日本語の入った係数ですが、2015年から毎年のように出題されているようですので、覚えておきましょう。
この減債基金係数を乗じて求めるものは、「毎年の積立金額」です。式で書くと、
【毎年の積立金額=将来の目標金額×減債基金係数】 となります。
分からない部分はどこかというと、毎年の積立額であり、分かっている将来の目標金額にこの係数を乗じるので、問題文(「毎年の積立額に乗じる」)とは少し違っています。
次に(2)年金現価係数ですが、「毎年の年金額(一定の金額)から年金原資(元本)を算出する際に利用」する係数とされます。
現価とは、現在価値のことになります。つまり、現在どのくらい年金原資(元本)があれば、それを運用しながら一定額の年金を受け取ることができるか、ということになります。
この年金現価係数を毎年の年金額に乗じて求めるものは、「現在どのくらい」の部分であり、「年金原資(元本)」です。式で書くと、
【年金原資(元本)=毎年の年金額×年金現価係数】 となります。
分からない数字の部分はどの部分かというと、年金原資であり、元本の部分です。
つまり毎年の年金額は分かっています。年金額は、「毎年受け取る金額」です。問題文を見ると、「毎年一定金額」と言っていてその部分は同じですが、問題文では、「積み立てた場合」の「元利合計」を求めようとしていますので、(2)の「受け取る」とは違うことがわかります
では、(3)年金終価係数をみてましょう。
これは、「毎年の積立金額から将来の目標金額を算出する際に利用」する係数とされています。
「終価」とは、将来価値になります。
式で表すと、【将来の目標金額=毎年の積立金額×年金終価係数】となります。
この年金終価係数を毎年の積立額に乗じて求めるものは、「将来の金額」です。
6つの係数の中で「終価」が入っているものは、「終価係数」と、この「年金終価係数」ですが、どちらの係数も、現在の金額や毎年積立てる金額に、係数を乗じることで、将来の価値を求めることができます。
問題文では、「一定期間経過後の元利合計額を試算する際、毎年の積立額に乗じる係数」とされていますので、どうやら、この係数が当てはまりそうです。
ここでは、この3つの係数を乗じて、つまり掛けることにより、何を求めることができるか、という見方をしましたが、逆に、その求めるもの、つまり「毎年の積立てる額」、「年金原資」、「将来の目標金額」が分かっている場合は、この3つの係数で除す、つまり割ってやると、今度は今まで係数を掛けてきた、それぞれ「将来の目標金額」、「毎年の年金額」、「毎年の積立金額」が算出されることになります。
また(1)の減債基金係数の式と(3)の年金終価係数の式は、係数以外は左右が入れ替わっているだけで似ていますね。(1)の減債基金指数は積み立てる額を、(3)の年金終価係数は目標金額を求めるものでであり、全体の姿も以下のように似ていますので、一緒に覚えておくといいかもしれません。
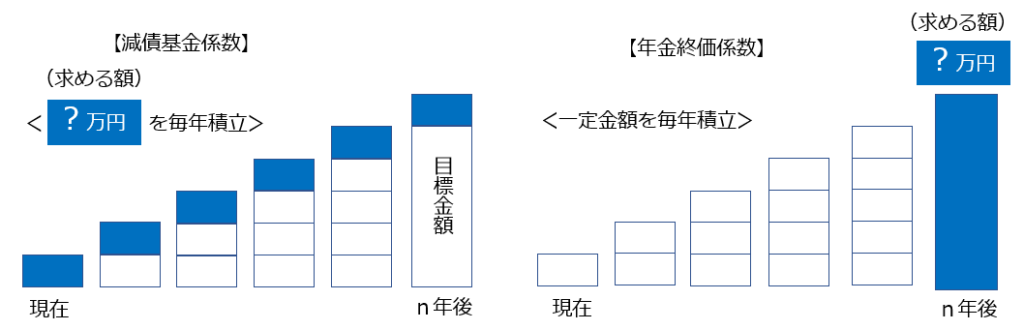
以上から、解答は次のようになります。
第2問(31)解答
一定の利率で複利運用しながら、毎年一定金額を積み立てた場合の一定期間経過後の元利合計額を試算する際、毎年の積立額に乗じる係数は、( )である。(1) 減債基金係数 ✕(2) 年金現価係数 ✕
(3) 年金終価係数 〇
追加解説
この問題で出て来なかった残りの3つの係数についても、見ておきましょう。
まず終価係数は、「現在の金額(元本)から将来の金額(終価)を算出する際に利用」する係数です。式で書くと、【将来の金額(終価)=現在額(元本)×終価係数】 となります。
次に現価係数は、「将来の金額から現在の金額(元本)(=現価)を算出する際に利用」する係数です。
式では、【現在額(元本)(=現価)=将来の金額×現価係数】となります。
そして最後に資本回収係数は、「年金原資から毎年の年金額を算出する際に利用」する係数です。
式で書くと、【毎年の年金額=年金原資×資本回収係数】となります。
6つの係数は、この「終価係数」と「現価係数」のように、比較的わかりやすいものもあります。
ただ、6つになると分かりにくくなるので、これを3つのパターンに分けてみてはどうでしょうか。
3つのパターンは、
①元本(現価)と目標額(終価)のどちらかを求める「終価係数」と「現価係数」の問題、
②毎年積立額と目標額(終価)のどちらかを求める「年金終価係数」か「減債基金係数」の問題、
③毎年受取額と元本額(現価)のちらかを求める「資本回収係数」と「年金現価係数」の問題、
に分けることができます。
ポイントは何を求めようとしているか
これではまだややこしいので、もう少し解きやすくまとめてみたいと思います。
ポイントは、「何を求めようとしているのか」という点です。係数の問題では、利率と期間は提示されていることが多いです。
そこで『求める答えは何か、で分ける』と、次の3つのパターンが見えてきます。
元本(現価)を求めるのか、もしくは毎年の額を求めるのか、あるいは目標額(終価)を求めるのか、の3つです。(毎年の額には、受取額と積立額の2つがありますが。)
この中で、元本(現価)、つまり初めの額が含まれているものは、上の①と③です。
目標額(終価)が分かっていて、元本(現価)を求めるのは、「現価係数」となります。
そして毎年の受取額が分かっていて、元本(現価)を求めるのは、「年金現価係数」となります。
ご覧のように、初めの額、元本を求める場合には、係数に「現価」の文字が付きます。
次に、目標額(終価)が含まれているのは、①と②です。つまり目標額(終価)を求める係数も2つだけということになります。
元本が分かっていて、目標額(終価)を求めるのは、「終価係数」となります。
また、毎年の積立額が分かっていて、目標額(終価)を求めるのは、「年金終価係数」となります。
「現価」と同じように、目標額を求める場合は、係数に「終価」の文字が付きます。
以上から、「毎年」の「受取額」や、「毎年」の「積立額」が分かっていて、元本や目標額を求める場合には、係数に「年金」が付くということが分かります。(「年金現価係数」と「年金終価係数」)
そして、その「毎年」の「受取額」や「積立額」が分からない場合、それを求める係数は残りの2つとなります。
「受取額」=「回収額」とするとイメージしやすいと思いますが、最初の原資が分かっていて、毎年の「受取額」を求める係数は、「資本回収係数」ということになります。
そして最後になりますが、目標額(終価)が決まっていて、「積立額」を求める係数が「減債基金係数」となります。
自分の経験では、「減債基金係数」が一番なじみのない言葉でしたので、覚えるのに苦労しました。
「減債」という言葉に「減る」という漢字を使いながら、目標額まで「増やすための」毎年の積立額を算出するための係数、ということですので、とてもイメージしずらかったです。
もともと「減債基金」とは、「公債や社債の発行者が円滑に償還を実施するために積み立てる資金」(出所:goo辞書)のことで、発行した債券の債務を減らすための基金、ということのようですが、これは特に覚える必要はないでしょう。
ですから、「減債基金係数」は、目標額まで積立てるためには、毎年いくら積立てればいいか計算するための係数、とそのまま覚えておいた方がいいように思います。
次回、もう一度、この6つの係数の問題を解いてみましょう。